THE FUTURE OF COMPUTING IS GEOMETRIC.


Master Symmetry Engine. “THE DIGITAL MIRROR” of the Torus³ Topology

The HyperMaze system began as an exploration of mathematical matrices, where simple numeric structures revealed hidden symmetries, entanglement patterns, and emergent behaviors. Over time, these discoveries evolved into a complete logic architecture that encodes information within fractal, holo-geometric frameworks. By modularizing each system of logic and functional component, HyperMaze transforms these principles into programmable and deterministic tools. The result is a hybrid computing platform where geometry, recursion, and self-similarity converge to deliver resilient compression, error correction, and context-aware processing. Designed for the next era of computing, HyperMaze offers a foundation that bridges classical and quantum principles through a unified, modular approach.
INFINITE SCALABILITY
Fractal architecture grows seamlessly to accommodate datasets of any size.
CONTEXT AWARE PROCESSING
Protect sensitive data while dynamically adapting to workload context.
SELF-HEALING FAULT TOLERANCE
Built-in geometric redundancy enables automatic recovery from large data loss.
HOLOGRAPHIC STORAGE
Encode and reconstruct data with using holo-geometric compression
LIGHTWEIGHT & MODULAR DESIGN
Deploy only the components you need organize dynamic and custom workflows.
CORE LOGIC








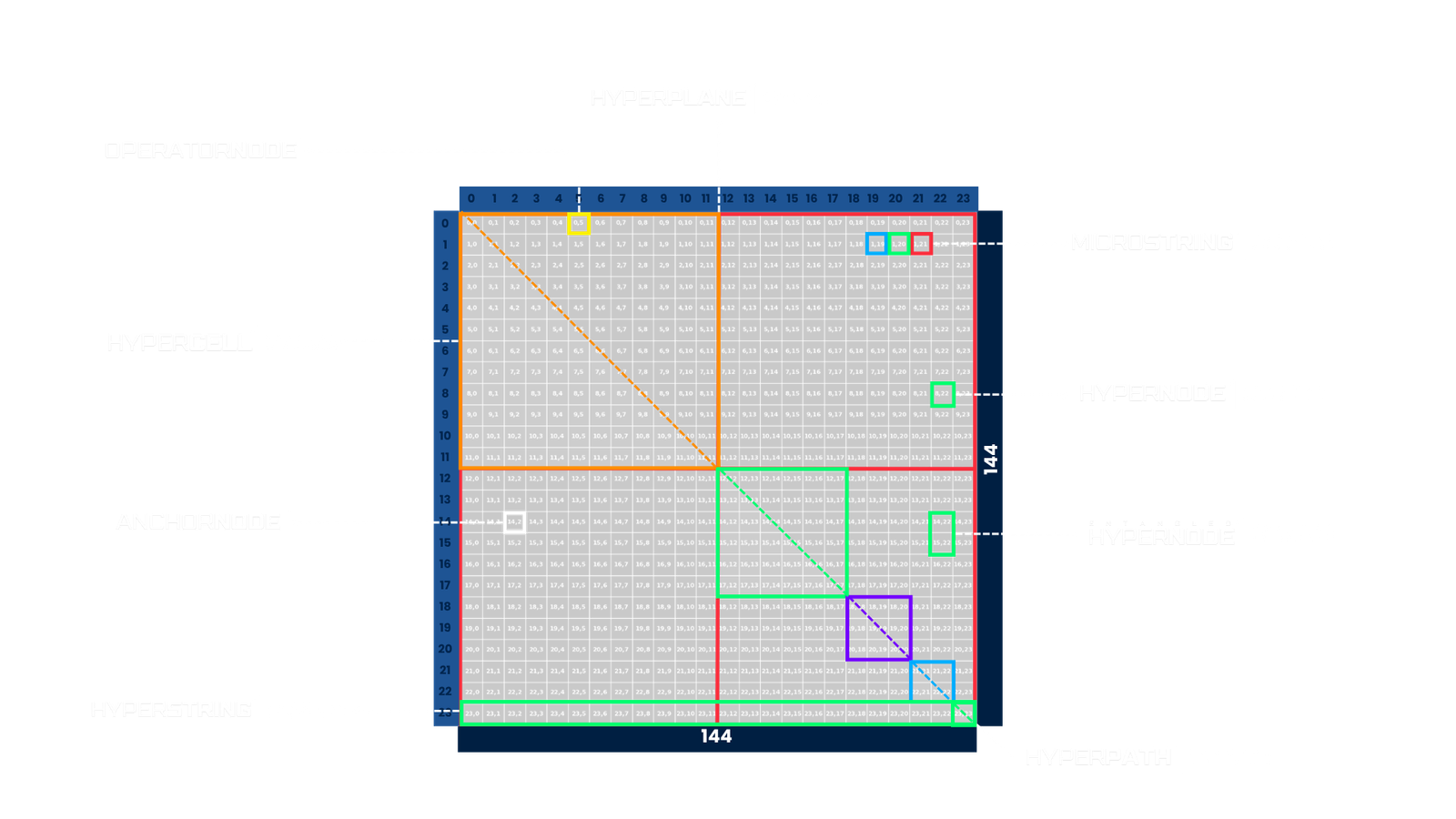
Torus³™ is a nonlinear information network and topological data field that encodes, transforms, and transmits information through coordinate relationships and strategic interdisciplinary mathematical rulesets. It operates across three integrated layers, structural encoding, circulant compression, and uniform verification to ensure stability and deterministic reconstruction across a multidimensional lattice.
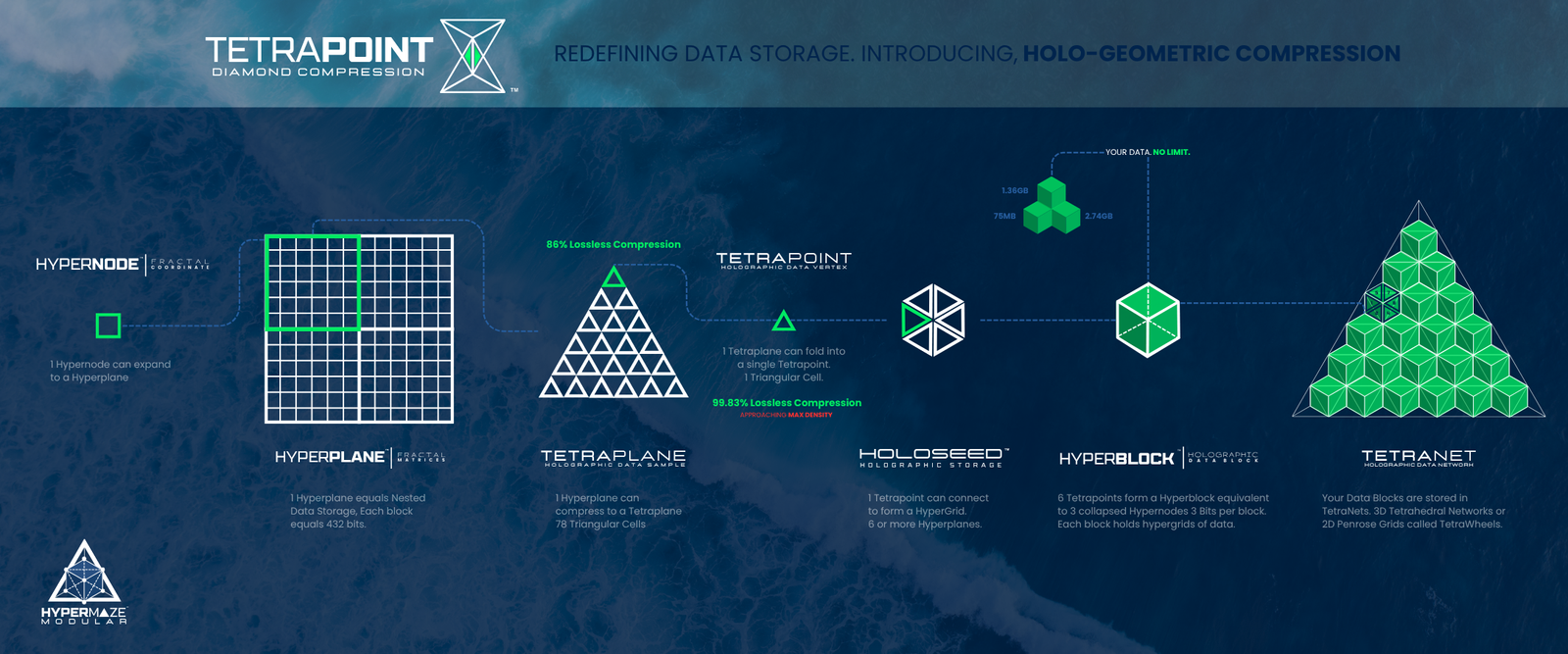
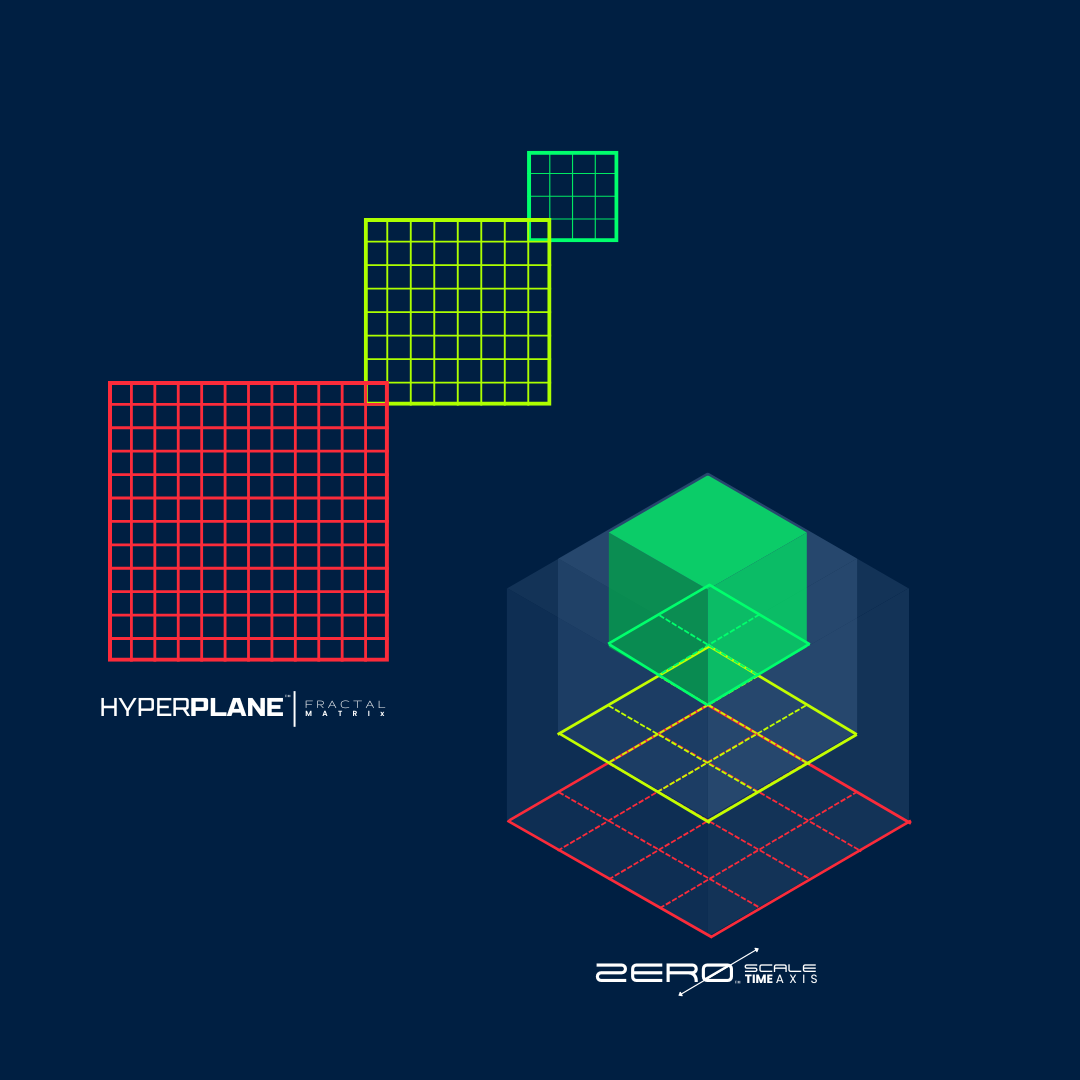
HyperGrid™ is the fractal matrix network that evolves simple HyperNodes into expansive HyperPlanes and nested HyperStructures. Each HyperNode encodes compact geometric and scalar relationships, which scale deterministically into higher-order grids without losing coherence. As these structures expand, they form multidimensional pathways for data routing, compression, and transformation. This progression enables the system to grow seamlessly from individual cells to complex, self-similar networks that maintain alignment, resilience, and computational efficiency at any scale.

GeoMapping™ provides the universal geometric reference that powers the Torus³™nonlinear data field. The GeoMesh™ unifies circular, square, and polygonal geometries into a single invariant lattice, enabling data to transform dynamically while preserving perfect spatial alignment across 2D and 3D vector space. This computational fabric supports holographic storage and integral scaling, allowing any fragment to reconstruct the whole without losing balance or coherence. As data compresses, expands, or shifts, the GeoMesh ensures structural invariance, making geometry an active engine for resilient, multidimensional computation.

SymetriTek™ is the master symmetry engine that enables the Torus³ topology to function as a self-referential and deterministic network. By embedding entangled logic, scalar channels, and mathematically grounded symmetric properties, SymetriTek ensures precise node alignment under structural transformations. It governs how data propagates and transforms across each geometric unit guaranteeing structural correspondence. Symetritek acts as a digital mirror providing resilient built in error correction, advanced data recovery, and emergent parity checks and verification functions that seamlessly promote data integrity across any operation or scale.

Fractal Zoom™ is the system’s multi-resolution controller, enabling data structures to dynamically expand or contract through deterministic fractal subdivisions. As a data block transitions from a simple cube into progressively finer shards, each resolution layer preserves perfect structural alignment and self-similarity. This allows any segment to be compressed for storage or scaled up for processing without loss of coherence or fidelity. By combining recursive fractal geometry with embedded resolution states, Fractal Zoom empowers the platform to adapt data density seamlessly, maintaining consistent logic and relationships across all scales and nested data fields. This is the holographic mechanism of the system as each shard retains enough information to reconstruct the entire original structure or dataset.

PATENT PENDING TECHNOLOGY
APPLICATIONS & USE CASES

ERROR CORRECTION
The HyperMaze system redefines fault tolerance through deterministic geometric encoding. Data is stored within fractal hyperplanes that mirror and entangle across layers, enabling entire matrices to regenerate from a single known node. Recursive logic cascades restore damaged structures, delivering high recovery rates even with extreme corruption, without relying on redundancy or backups.

ENCRYPTION PROTOCOL
HyperMaze™ Encryption embeds data in time evolving fractal matrices, producing dynamic encryption keys that continuously shift along scalar timelines. Unlike static cryptographic systems, this approach resists quantum attacks and brute-force decryption by requiring precisely sequenced inverse transformations. Security becomes a moving target, uncompromised through conventional methods.

DATA COMPRESSION
TetraPoint™ Diamond Compression reduces data by folding hyperplanes into smaller tetrahedral cells, maintaining structural integrity and coordinate mapping. This geometric approach achieves 78-99% lossless compression, transforming large datasets into compact holographic seeds. Compressed structures remain fully reconstructible, enabling extreme data density without compromising fidelity.

DATA PROCESSING
HyperMaze™ processes information through dynamic hypergrids that reconfigure in real time. Nodes compress, expand, and route data simultaneously, reducing latency while preserving deterministic logic. This enables scalable analytics and transformation pipelines that self-optimize as data flows. This is ideal for high-throughput applications.

AI & MACHINE LEARNING
Diamond Mind™ AI trains and compresses domain-specific datasets into Tetrapoints stored in the TetraNet. When a query is received, HyperLinks dynamically activate the most relevant memory banks, allowing the Thought Composer™ engine to cross-reference and recall information across multiple datasets, producing highly contextual answers with minimal latency.

GRAPHICS RENDERING
HyperVerse™ replaces discrete level-of-detail transitions with recursive fractal subdivision, delivering smooth, continuous scaling in immersive environments. Each surface encodes a compact rule set that unfolds or collapses seamlessly, eliminating visual popping and streaming lag. Volumetric depth layers enrich realism while maintaining GPU efficiency.
SYSTEM AXIOMS
PRINCIPLE 1: NATURAL SYSTEMS | Nature encodes intelligence through geometry. The Hypermaze draws inspiration from natural lattices, embedding information within self-organizing structures that mimic biological resilience and efficiency.
PRINCIPLE 2: PATTERN RECOGNITION | Order emerges from complexity. By weaving predictable numeric and geometric patterns into every layer, the system can recognize, reconstruct, and correct information without external intervention.
PRINCIPLE 1: MATH IS THE FOUNDATION, NUMBERS ARE THE INTERFACE | Math is the fabric of the Hypermaze. Deterministic algorithms based on modular arithmetic, symmetry, and number theory transform raw data into structured geometric relationships.
PRINCIPLE 4: EMERGENCE IS A RESULT | Nature encodes intelligence through geometry. The Hypermaze draws inspiration from natural lattices, embedding information within self-organizing structures that mimic biological resilience and efficiency.
HOW IT WORKS

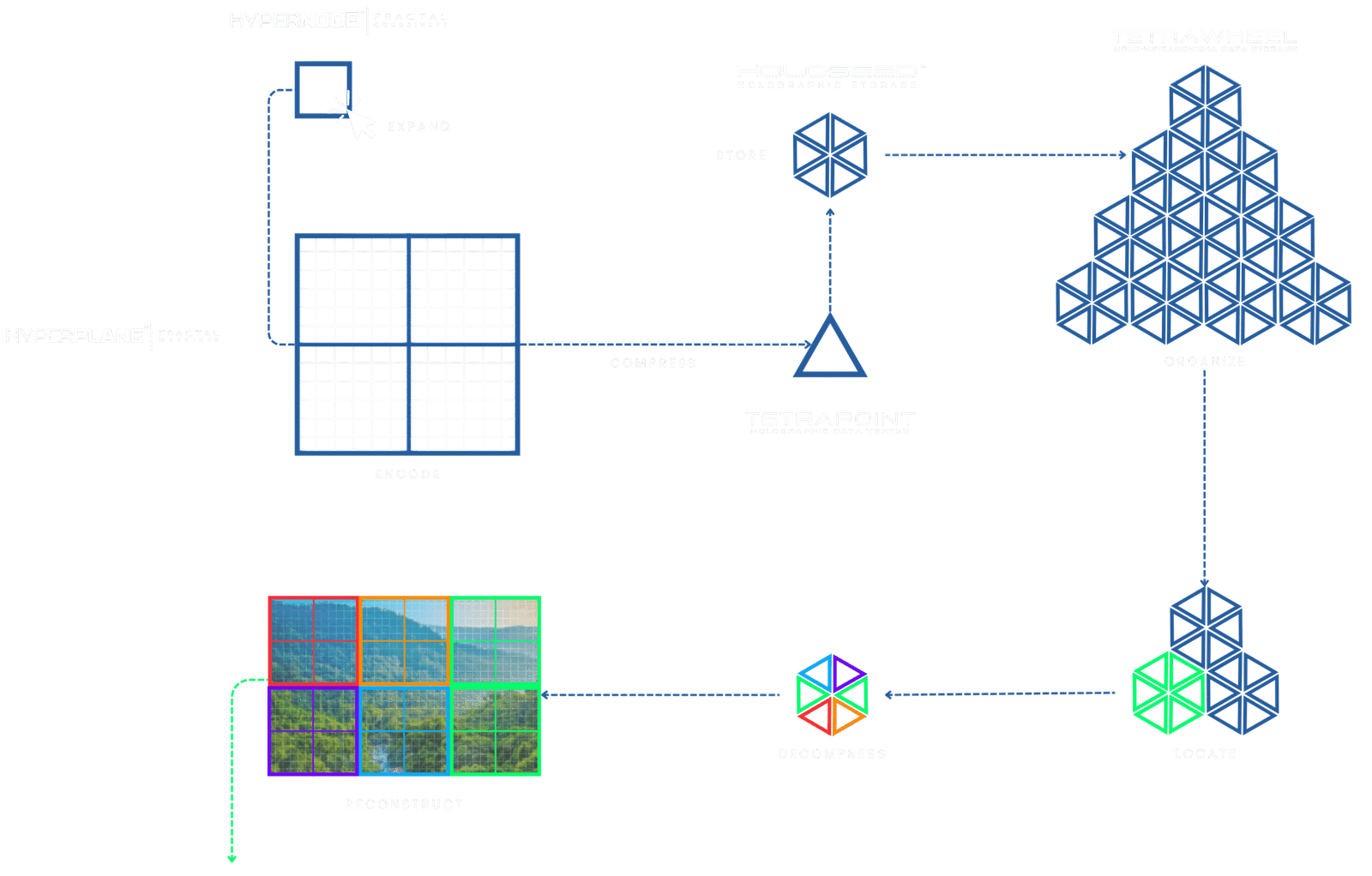
This visualization illustrates the complete lifecycle of data within the HyperMaze system. A single HyperNode first expands into a structured HyperPlane using the Error Correction algorithm and Seed Node to establish a precise geometric framework. Within this lattice, an image or dataset is encoded, leveraging symmetry pathways to distribute information predictably across the matrix. The Tetrapoint Diamond Compression algorithm then remaps and reduces the data into a compact Tetraplane data sample before further collapsing it into a single Tetrapoint—a highly condensed, lossless holographic unit of storage. Multiple Tetrapoints are organized into a Holoseed, an integrated seed structure that preserves all original information in a deterministic scalar configuration. These Holoseeds are systematically stored within the TetraNet, a dynamic tetrahedral data network. When retrieval is needed, any Holoseed can be selected, decompressed, and reconstructed back to its original state, enabling efficient, lossless storage and retrieval in a scalable geometric system.

GEOMETRIC MODULES




Modular square matrices that encode numeric and spatial relationships into deterministic coordinate grids. They maintain coordinate invariance across transformations, providing a stable reference frame for all higher-order geometric operations.

Triangular modules formed by folding and compressing HyperGrid structures into resilient geometric shards. These shards maintain coordinate invariance and logical integrity by remapping relational data across nested triangular lattices.

Cyclic configurations that organize spatial coherence between nodes. Intralayer cycles and permutations expand or compress vector space, producing emergent interlayer replicas that can be deterministically altered by systematic operations.
INTERDISCIPLINARY APPROACH
Modular Arithmetic
Deterministic Number Patterns
Group
Theory
Symmetric transformations
Fractal Geometry
Infinite self-similarity across scales.
Holographic Principles
The whole encoded in every part.
Topological Systems
Continuity and adaptive connectivity.
Number Theory
Intrinsic structure of information.
Graph
Theory
Networks of relational intelligence.
Cellular Automata
Emergent complexity from simple rules.
Relational Geometry
Spatial encoding of computation & memory.
Nonlinear Dynamics
Pattern formation in complex systems.
Habitant potenti commodo auctor finibus ullamcorper phasellus proin erat tristique
Habitant potenti commodo auctor finibus ullamcorper phasellus proin erat tristique
Habitant potenti commodo auctor finibus ullamcorper phasellus proin erat tristique
Habitant potenti commodo auctor finibus ullamcorper phasellus proin erat tristique